2 в 63 степени, Расшифровка степеней защиты IP
Сейчас увидите. Примеры таких устройств: многофункциональные кабельные тестеры, влагозащищенные кондуктометры, светодиодные приборы, счетчики воды, оксиметры, пирометры. Есть еще один быстрый хак.
Примеры таких устройств: печатная плата работающая без корпуса , электропровод без оболочки и т. Электрооборудование со степенью защиты IP10 может использоваться в закрытых помещениях, доступ в которые разрешается только уполномоченным на это и обученным лицам. Примеры таких устройств: мультиметры, электрические измерительные приборы, предназначенные для помещения в защищенные короба, потолочные светильники, источники бесперебойного питания, усилители.
Электрооборудование со степенью защиты IP20 может использоваться в обычных помещениях с наличием только крупных частиц, осаждаемых на вертикальных поверхностях. Такими помещениями являются теплый сухой цех, театр, офис, магазин и т. Примеры таких устройств: светильники для внутреннего и внешнего освещения, установленные во влагозащищенных корпусах, в охранно-пожарных приёмно-контрольных приборах, розетка открытой установки и т. Примеры таких устройств: электрический конвектор отопления, клавишный переключатель электрических цепей, розетки, преобразователи частоты и т.
Примеры таких устройств: светодиодные осветительные устройства, судовые электроконвекторы, блоки питания светодиодных лент и т. Примеры таких устройств: специализированные светодиодные осветительные устройства, такие как уличные светильники. Примеры таких устройств: конвекторы, используемые для обогрева ванных комнат и подобных помещений, осветительные приборы, вентиляционные системы, специализированные осветительные устройства — например, на станциях с прохождением транспортных средств.
Электрооборудование со степенью защиты IP30 может использоваться в сухих помещениях с осаждением частиц на вертикальных частях или на недоступных горизонтальных плоскостях.
Нельзя допускать попадания влаги. Примеры таких устройств: распределительные шкафы, компактные пластиковые кожухи, источники бесперебойного питания, навесные распределительные шкафы, защитные пластиковые корпуса.
Примеры таких устройств: терморегуляторы систем «теплый пол», ящики с понижающим трансформаторным напряжением В, шкафы учета, электромеханические напольные шкафы и т. Примеры таких устройств: ящики силовые, выключатели нагрузки, пластиковые защитные кожухи, защитные пластиковые корпуса для электрооборудования. Примеры таких устройств: светодиодные ленты, некоторые потолочные светильники, сигнализаторы давления, распределительные приборы и т.
Примеры таких устройств: приборы фазировки, светодиодные модули, такие как панели заливного света, бытовые вытяжные вентиляторы, акустические системы и т. Электрооборудование со степенью защиты IP40 может использоваться в обычных сухих помещениях с осаждением частиц даже на недоступных плоскостях.
Примеры таких устройств: LED-светильники, устройства нормирования сигналов, настенные шкафы навесного монтажа, пластиковые корпуса измерительных приборов, сигнальные лампы, лазерные измерительные приборы.
Примеры таких устройств: LED-светильники, устройства нормирования сигналов, настенные шкафы навесного монтажа, пластиковые корпуса измерительных приборов, встраиваемые пластиковые боксы, монтажные коробки.
Примеры таких устройств: технический манометр, распределительные коробки открытой установки, настенные шкафы навесного монтажа, пластиковые корпуса измерительных приборов, встраиваемые пластиковые боксы, монтажные коробки. Примеры таких устройств: технические манометры, технические барометры, пожарные извещатели, пластиковые корпуса измерительных приборов, встраиваемые пластиковые боксы, монтажные коробки. Примеры таких устройств: технические манометры, технические барометры, пожарные извещатели, кабельные тестеры, фотореле, панельные вилки, пластиковые корпуса электроприборов, розеток, встраиваемые пластиковые боксы.
Примеры таких устройств: технические манометры, технические барометры, пожарные извещатели, UV-ловушки для насекомых, наборы для трассировки кабелей, панельные вилки, пластиковые корпуса электроприборов, розеток, встраиваемые пластиковые боксы.
Примеры таких устройств: тумблеры, нажимные кнопки, светодиодные светильники, мультиметры, пластиковые защитные кожухи, защитные пластиковые корпуса для электрооборудования. Примеры таких устройств: электросчетчики, цифровые индикаторы, поворотные камеры, приборы учета, пластиковые защитные кожухи, защитные пластиковые корпуса для электрооборудования.
Примеры таких устройств: пожарные извещатели, UV-ловушки для насекомых, защищенные мультиметры, тепловизоры, пластиковые корпуса электроприборов, розеток, встраиваемые пластиковые боксы, тестеры витой пары. Примеры таких устройств: технические манометры, защищенные мультиметры, тепловизоры, пластиковые корпуса электроприборов, розеток, встраиваемые пластиковые боксы, тестеры витой пары, светосигнальные светодиодные приборы. Примеры таких устройств: технические манометры, защищенные мультиметры, лазерные нивелиры, ультразвуковые тепломеры, встраиваемые пластиковые боксы, тестеры витой пары.
Примеры таких устройств: защищенные мультиметры, лазерные нивелиры, ультразвуковые тепломеры, защитные корпуса электроприборов, многофункциональные кабельные тестеры. Примеры таких устройств: промышленные конвекторы, ультразвуковые тепломеры, защитные корпуса электроприборов, многофункциональные кабельные тестеры, водонепроницаемые выключатели. Примеры таких устройств: защищенные мультиметры, ультразвуковые тепломеры, защитные корпуса электроприборов, многофункциональные кабельные тестеры, водонепроницаемые выключатели, радиостанции.
Примеры таких устройств: технические манометры, защищенные мультиметры, встраиваемые пластиковые боксы, тестеры витой пары, приборы управления доступом и охранной сигнализацией. Примеры таких устройств: многофункциональные кабельные тестеры, приборы управления доступом и охранной сигнализацией, специализированные светильники, влагозащищенные кондуктометры. Примеры таких устройств: многофункциональные кабельные тестеры, специализированные видеорегистраторы, влагозащищенные кондуктометры, светодиодные приборы.
Примеры таких устройств: многофункциональные кабельные тестеры, влагозащищенные кондуктометры, светодиодные приборы, счетчики воды, оксиметры, пирометры. Примеры таких устройств: многофункциональные кабельные тестеры, влагозащищенные кондуктометры, светодиодные приборы, счетчики воды, водонепроницаемые пьезоэлектрические элементы, подводные камеры. На нашем сайте мы используем cookie для сбора информации технического характера.
Главная идея доказательства — наличие сколь угодно больших по абсолютной величине как положительных, так и отрицательных слагаемых. Попробуйте выполнить доказательство сами. Интересно понаблюдать за последними цифрами членов последовательности степеней двойки.
Так как каждое последующее число последовательности получается удвоением предыдущего, то последняя цифра каждого из них полностью определяется последней цифрой предыдущего числа.
А так как различных цифр ограниченное количество, последовательность последних цифр степеней двойки просто обязана быть периодической! Длина периода, естественно, не превышает 10 поскольку именно столько цифр мы используем , но это сильно завышенное значение.
Попробуем оценить его, не выписывая пока саму последовательность. Ясно, что последние цифры всех степеней двойки, начиная с 2 1 , четные. Кроме того, среди них не может быть нуля — потому что число, оканчивающееся нулем, делится на 5, в чем заподозрить степени двойки никак нельзя. А так как четных цифр без нуля имеется всего четыре, то и длина периода не превосходит 4. Проверка показывает, что так оно и есть, причем периодичность проявляется почти сразу: 1, 2, 4, 8, 6, 2, 4, 8, 6, Не менее успешно можно оценить и длину периода последней пары цифр последовательности степеней двойки.
Так как все степени двойки, начиная с 2 2 , делятся на 4, то и числа, образованные их последними двумя цифрами, делятся на 4. Не более чем двузначных чисел, делящихся на 4, имеется всего 25 для однозначных чисел предпоследней цифрой считаем ноль , но из них надо выбросить пять чисел, оканчивающихся нулем: 00, 20, 40, 60 и Проверка показывает, что так и есть, начинается период с числа 2 2 и содержит пары цифр: 04, 08, 16, 32, 64, 28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, 44, 88, 76, 52, а затем опять 04 и так далее.
Итак, на последние цифры степеней двойки наложены довольно жесткие ограничения. А как насчет первых цифр? Здесь ситуация практически противоположная. Оказывается, для любого набора цифр первая из которых — не ноль найдется степень двойки, начинающаяся с этого набора цифр.
И таких степеней двойки бесконечно много! Например, существует бесконечное количество степеней двойки, начинающихся с цифр или, скажем, 3 А если рассмотреть только одну самую первую цифру различных степеней двойки — какие значения она может принимать? Нетрудно убедиться, что любые — от 1 до 9 включительно нуля среди них, естественно, нет.
Но какие из них встречаются чаще, а какие реже? Как-то сразу не видно причин, по которым одна цифра должна встречаться чаще другой. Однако более глубокие размышления показывают, что как раз равной встречаемости цифр ожидать не приходится.
Действительно, если первая цифра какой-либо степени двойки есть 5, 6, 7, 8 или 9, то первая цифра следующей за ней степени двойки будет обязательно единицей! Поэтому должен иметь место «перекос», по крайней мере, в сторону единицы.
Следовательно, вряд ли и остальные цифры будут «равнопредставленными». Практика а именно — прямой компьютерный расчет для первых нескольких десятков тысяч степеней двойки подтверждает наши подозрения. Вот какова относительная доля первых цифр степеней двойки с округлением до 4 знаков после запятой:. Как видим, с ростом цифр эта величина убывает и потому та же единица примерно в 6,5 раз чаще бывает первой цифрой степеней двойки, чем девятка.
Как ни покажется странным, но практически такое же соотношение количеств первых цифр будет иметь место почти для любой последовательности степеней — не только двойки, но, скажем, и тройки, пятерки, восьмерки и вообще почти любого числа, в том числе и нецелого исключение составляют лишь некоторые «особые» числа. Причины этого весьма глубоки и непросты, и для их уяснения надо знать логарифмы. Используя упомянутую выше связь между степенями двойки и пятерки, А. Канель обнаружил интересное явление.
Давайте из последовательности первых цифр степеней двойки 1, 2, 4, 8, 1, 3, 6, 1, 2, 5, Оказывается, эти цифры непременно встретятся тоже подряд , начиная с некоторого места, в последовательности первых цифр степеней пятерки. Степени двойки также являются своеобразным «генератором» для производства широко известных совершенных чисел , которые равны сумме всех своих делителей, за исключением себя самого.
Например, у числа 6 четыре делителя: 1, 2, 3 и 6. Отбросим тот, который равен самому числу 6. Поэтому 6 — совершенное число. Для получения совершенного числа возьмем две последовательные степени двойки: 2 n —1 и 2 n.
Уменьшим большую из них на 1, получим 2 n — 1. Оказывается, если это — простое число, то, домножив его на предыдущую степень двойки, мы образуем совершенное число 2 n —1 2 n — 1. Нечетные совершенные числа пока не обнаружены и мало кто верит в их существование. Тесную связь имеют степени двойки с так называемыми числами Каталана , последовательность которых имеет вид 1, 1, 2, 5, 14, 42, , Они часто возникают при решении различных комбинаторных задач.
Например, сколькими способами можно разбить выпуклый n -угольник на треугольники непересекающимися диагоналями?
Последовательность чисел Каталана имеет множество любопытных свойств, и одно из них как раз связанное с темой этой статьи заключается в том, что порядковые номера всех нечетных чисел Каталана являются степенями двойки! Степени двойки нередко встречаются в различных задачах, причем не только в условиях, но и в ответах. Возьмем, например, популярную когда-то да и поныне не забытую Ханойскую башню. Так называлась игра-головоломка, придуманная в XIX веке французским математиком Э.
Она содержит три стержня, на один из которых надето n дисков с отверстием в середине каждого. Диаметры всех дисков различны, и они расположены в порядке убывания снизу вверх, т. Получилась как бы башня из дисков. Требуется перенести эту башню на другой стержень, соблюдая такие правила: перекладывать диски строго по одному снимая верхний диск с любого стержня и всегда класть только меньший диск на больший, но не наоборот. Спрашивается: какое наименьшее число ходов для этого потребуется?

Ходом мы называем снятие диска с одного стержня и надевание его на другой. Ответ: оно равно 2 n — 1, что легко доказывается по индукции.

Пусть для n дисков потребное наименьшее число ходов равно X n. В процессе работы рано или поздно придется снимать самый большой диск со стержня, на который первоначально были надеты все диски. Так как этот диск можно надевать только на пустой стержень иначе он «придавит» меньший диск, что запрещено , то все верхние n дисков придется предварительно перенести на третий стержень. Для этого потребуется не меньше X n ходов. Далее переносим наибольший диск на пустой стержень — вот еще один ход.
Наконец, чтобы сверху его «притиснуть» меньшими n дисками, опять потребуется не меньше X n ходов. Получено рекуррентное соотношение, но для того чтобы его привести к «нормальному» виду, надо еще найти X 1.
Найдите все натуральные числа, которые нельзя представить в виде суммы нескольких не менее двух последовательных натуральных чисел. Давайте проверим сначала наименьшие числа. Ясно, что число 1 в указанном виде непредставимо. Зато все нечетные, которые больше 1, представить, конечно, можно. А как обстоят дела с четными числами? Легко убедиться, что числа 2 и 4 нельзя представить в требуемом виде.
Может, и для всех четных чисел так? Зато число 8 опять не поддается. Что ж, накопленная информация позволяет сделать предварительные выводы. Обратите внимание: не удалось представить в указанном виде только степени двойки. Верно ли это для остальных чисел? Оказывается, да! В самом деле, рассмотрим сумму всех натуральных чисел от m до n включительно.
Как известно, сумма последовательных членов арифметической прогрессии а ведь именно с ней мы имеем дело! Заметим, что в числителе находятся два сомножителя, каждый из которых строго больше 1, и при этом четность их — различна. Выходит, что сумма всех натуральных чисел от m до n включительно делится на нечетное число, большее 1, и потому не может быть степенью двойки.
Так что теперь понятно, почему не удалось представить степени двойки в нужном виде. Осталось убедиться, что не степени двойки представить можно. Что касается нечетных чисел, то с ними мы уже разобрались выше. Возьмем какое-либо четное число, не являющееся степенью двойки. Пусть наибольшая степень двойки, на которую оно делится, это 2 a a — натуральное. А вот еще одна задача впервые ее предложил В. Произволов, но в несколько иной формулировке :.
Садовый участок окружен сплошным забором из N досок. Согласно приказу тети Полли Том Сойер белит забор, но по собственной системе: продвигаясь всё время по часовой стрелке, сначала белит произвольную доску, затем пропускает одну доску и белит следующую, затем пропускает две доски и белит следующую, затем пропускает три доски и белит следующую, и так далее, каждый раз пропуская на одну доску больше при этом некоторые доски могут быть побелены несколько раз — Тома это не смущает. Том считает, что при такой схеме рано или поздно все доски будут побелены, а тетя Полли уверена, что хотя бы одна доска останется непобеленной, сколько бы Том ни работал.
При каких N прав Том, а при каких — тетя Полли? Описанная система побелки представляется довольно хаотичной, поэтому первоначально может показаться, что для любого или почти любого N каждой доске когда-нибудь достанется своя доля известки, т.
Но первое впечатление обманчиво, потому что на самом деле Том прав только для значений N , являющихся степенями двойки. Для остальных N найдется доска, которая так и останется навеки непобеленной. Доказательство этого факта довольно громоздко хотя, в принципе, несложно. Предлагаем читателю выполнить его самому. Вот каковы они — степени двойки. С виду — проще простого, а как копнешь И затронули мы здесь далеко не все удивительные и загадочные свойства этой последовательности, а лишь те, что бросились в глаза.
Ну, а читателю предоставляется право самостоятельно продолжить исследования в этой области. Несомненно, они окажутся плодотворными. Более вероятно, что для мудреца все закончилось длительным тюремным заключением по статье «за наглость».
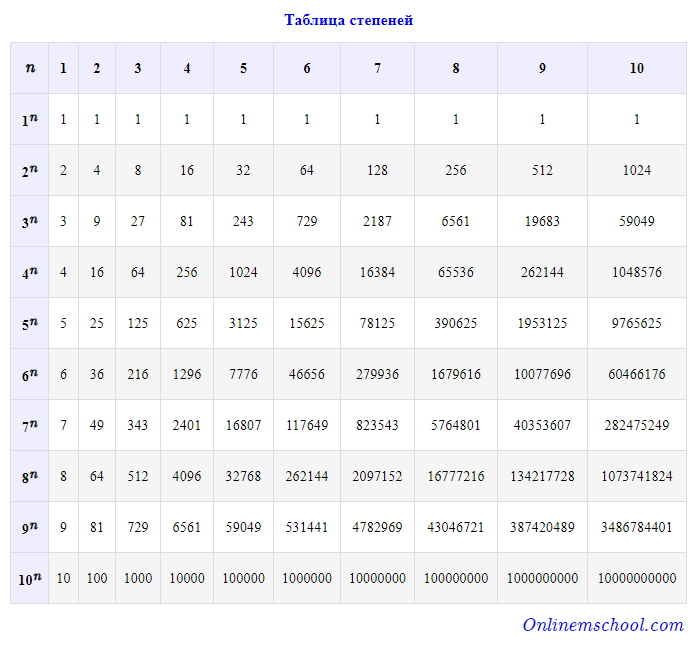
Только вместо степеней двойки используются степени десятки потому она так и называется , а цифры в записи показывают, в каком количестве очередную степень десятки надо прибавлять. Болтянского «Часто ли степени двойки начинаются с единицы? Оно содержит свыше 18 миллионов цифр. Закрыть Новости науки.
Большой адронный коллайдер. Результаты LHC. Загадки LHC. Двухфотонный всплеск ГэВ. LHC в работе. Общее расписание. Ранние этапы. Результаты работы LHC в году. Сеанс LHC Run 1. Сеанс LHC Run 2. Сеанс LHC Run 3. Устройство и задачи LHC. Устройство LHC. Задачи LHC. Свойства адронов. Поиск бозона Хиггса. Физика элементарных частиц. Величины и единицы. Как изучают частицы.
Эксперименты на коллайдерах. Стандартная модель. Хиггсовский механизм.